Leaving Cert Geometry

Defintions

 

Adapted from Geometry Syllabus, Appendix 1

 

 

 

Definitions

 

1

The line segment [AB] is the part of the line AB between A and B (including the endpoints). The point A divides the line AB into two pieces, called rays. The point A lies between all points of one ray and all points of the other. We denote the ray that starts at A and passes through B by [AB. Rays are sometimes referred to as half-lines.

 

2

If three or more points lie on a single line, we say they are collinear.

 

3

Let A, B and C be points that are not collinear. The triangle ∆ABC is the piece of the plane enclosed by the three line segments [AB], [BC] and [CA]. The segments are called its sides, and the points are called its vertices (singular vertex).

 

4

We denote the distance between the points A and B by |AB|. We define the length of the segment [AB] to be |AB|.

 

5

The midpoint of the segment [AB] is the point M of the segment with |AM| = |MB| =

                                                  

 

6

A subset of the plane is convex if it contains the whole segment that connects any two of its points.

For example, one side of any line is a convex set, and triangles are convex sets.

We do not define the term angle formally. Instead we say: There are things called angles. To each angle is associated:

1. a unique point A, called its vertex;

2. two rays [AB and [AC, both starting at the vertex, and called the arms of the angle;

3. a piece of the plane called the inside of the angle.

An angle is either a null angle, an ordinary angle, a straight angle, a reflex angle or a full angle. Unless otherwise specified, you may take it that any angle we talk about is an ordinary angle.

 

7

An angle is a null angle if its arms coincide with one another and its inside is the empty set.

 

8

An angle is an ordinary angle if its arms are not on one line, and its inside is a convex set.

 

9

An angle is a straight angle if its arms are the two halves of one line, and its inside is one of the sides of that line.

 

10

An angle is a reflex angle if its arms are not on one line, and its inside is not a convex set.

 

11

An angle is a full angle if its arms coincide with one another and its inside is the rest of the plane.

 

12

Suppose that A, B, and C are three noncollinear points. We denote the (ordinary) angle with arms [AB and [AC by  (and also by ). We shall also use the notation  to refer to straight angles, where A, B, C are collinear, and A lies between B and C (either side could be the inside of this angle).

Sometimes we want to refer to an angle without naming points, and in that case we use lower-case greek letters, α, β, γ,  etc.

 

13

The ray [AD is the bisector of the angle  if

| |= || =

                                       

 

14

A right angle is an angle of exactly 90o

 

15

An angle is acute if it has less than 90o, and obtuse if it has more than 90o.

 

16

If  is a straight angle, and D is off the line BC, then  and  are called supplementary angles. They add to 180o.

 

17

When two lines AB and AC cross at a point A, they are perpendicular if  is a right angle.

 

18

Let A lie between B and C on the line BC, and also between D and E on the line DE. Then and  are called vertically-

opposite angles.

 

19

Let A, B, C and Á, B´, C´ be triples of non-collinear points.

We say that the triangles ∆ABC and ∆A´B´C´ are congruent if all the sides and angles of one are equal to the corresponding sides and angles of the other,

i.e. |AB| = |A´B´|, |BC| = |B´C´|, |CA| = |C´A´|, || = |  A´B´C´|,

|| = |B´C´A´|, and || = |C´A´B´|. See Figure 2.

20

A triangle is called right-angled if one of its angles is a right angle. The other two angles then add to 90o, by Theorem 4, so are both acute angles. The side opposite the right angle is called the hypotenuse.

 

21

A triangle is called isosceles if two sides are equal. It is equilateral if all three sides are equal. It is scalene if no two sides are equal.

 

22

Two lines l and m are parallel if they are either identical, or have no common point.

 

23

If l and m are lines, then a line n is called a transversal of l and m if it meets them both.

 

24

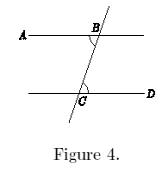
Given two lines AB and CD and a transversal BC of them, as in Figure 4, the angles  and  are called alternate angles.

25

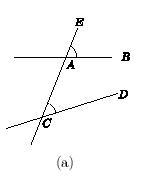
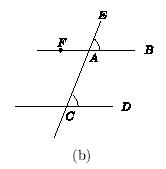
Given two lines AB and CD, and a transversal AE of them, as in Figure 8(a), the angles  and  are called corresponding angles

Figure 8

26

In Figure 9, the angle α is called an exterior angle of the triangle, and the angles β and γ are called (corresponding) interior opposite angles.

27

The perpendicular bisector of a segment [AB] is the line through the midpoint of [AB], perpendicular to AB.

 

28

A closed chain of line segments laid end-to-end, not crossing anywhere, and not making a straight angle at any endpoint encloses a piece of the plane called a polygon. The segments are called the sides or edges of the polygon, and the endpoints where they meet are called its vertices.

Sides that meet are called adjacent sides, and the ends of a side are called adjacent vertices. The angles at adjacent vertices are called adjacent

angles.

 

29

A quadrilateral is a polygon with four vertices.

Two sides of a quadrilateral that are not adjacent are called opposite sides. Similarly, two angles of a quadrilateral that are not adjacent are called opposite angles.

 

30

A rectangle is a quadrilateral having right angles at all four vertices.

 

31

A rhombus is a quadrilateral having all four sides equal.

 

32

A square is a rectangular rhombus.

 

33

A polygon is equilateral if all its sides are equal, and regular if all its sides and angles are equal.

 

34

A parallelogram is a quadrilateral for which both pairs of opposite sides are parallel.

 

35

If the three angles of one triangle are equal, respectively, to those of another, then the two triangles are said to be similar.

 

36

Let s and t be positive real numbers. We say that a point C divides the segment [AB] in the ratio s : t if C lies on the line AB,

and is between A and B,

and

We say that a line l cuts [AB] in the ratio s : t if it meets AB at a point

C that divides [AB] in the ratio s : t.

 

37

If one side of a triangle is chosen as the base, then the opposite vertex is the apex corresponding to that base. The corresponding height is the length of the perpendicular from the apex to the base. This perpendicular segment is called an altitude of the triangle.

 

38

The area of a triangle is half the base by the height.

 

39

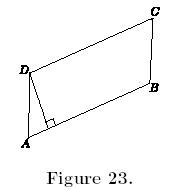
Let the side AB of a parallelogram ABCD be chosen as a base (Figure 23). Then the height of the parallelogram corresponding to that base is the height of the triangle _ABC.

40

A circle is the set of points at a given distance (its radius) from a fixed point (its centre). Each line segment joining the centre to a point of the circle is also called a radius. The plural of radius is radii. A chord is the segment joining two points of the circle. A diameter is a chord through the centre. All diameters have length twice the radius. This number is also called the diameter of the circle.

Two points A, B on a circle cut it into two pieces, called arcs. You can specify an arc uniquely by giving its endpoints A and B, and one other point C that lies on it. A sector of a circle is the piece of the plane enclosed by an arc and the two radii to its endpoints.

The length of the whole circle is called its circumference. For every circle, the circumference divided by the diameter is the same. This ratio is

called π.

A semicircle is an arc of a circle whose ends are the ends of a diameter.

Each circle divides the plane into two pieces, the inside and the outside.

The piece inside is called a disc.

If B, and C are the ends of an arc of a circle, and A is another point, not on the arc, then we say that the angle is the angle at A standing on the arc. We also say that it stands on the chord [BC].

 

41

A cyclic quadrilateral is one whose vertices lie on some circle.

 

42

The line l is called a tangent to the circle S when l S has exactly one point. The point is called the point of contact of the tangent.

 

43

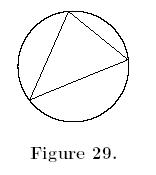
The circumcircle of a triangle ∆ABC is the circle that passes through its vertices (see Figure 29). Its centre is the circumcentre of the triangle, and its radius is the circumradius.

44

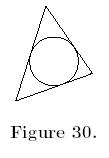
The incircle of a triangle is the circle that lies inside the triangle and is tangent to each side (see Figure 30). Its centre is the incentre, and its radius is the inradius.

45

A line joining a vertex of a triangle to the midpoint of the opposite side is called a median of the triangle. The point where the three medians meet is called the centroid.

 

46

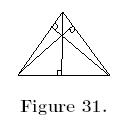
The point where the perpendiculars from the vertices to the opposite sides meet is called the orthocentre (see Figure 31).

Note: The official version of Project Maths material may be found through the Project Maths website www.projectmaths.ie

Page created by Neil Hallinan © 2010