Drawing on Pythagoras

Project: To illustrate Pythagoras Theorem by drawing on squared paper

Resources:

Squared paper (from a Sum Copy)

Pencil

Ruler

Calculator

Stage 1: Draw a St. Brigid’s Cross shape.

Complete the square by joining the end points.

A convenient method of drawing the square on the hypotenuse is to start at a ‘centre’ point and draw continuously using the lengths of the sides of the triangle following the arrows as illustrated.

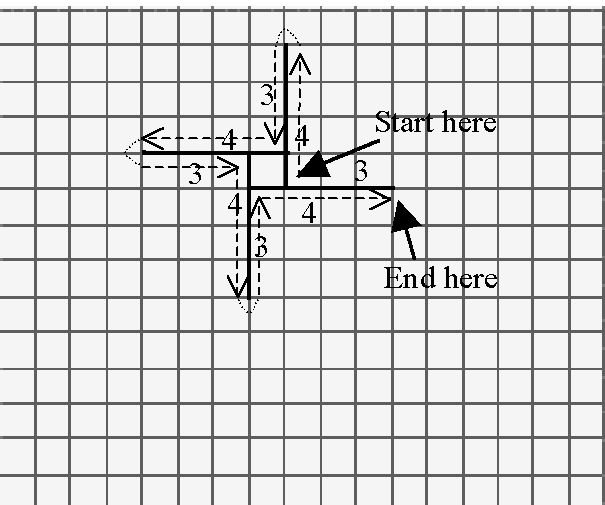
Figure 1

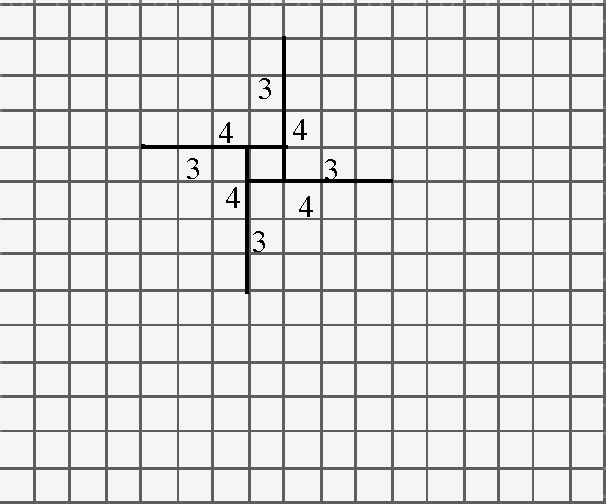
Figure 2

Figure 3

Stage 2: Attach the fifth triangle with its hypotenuse against the side of the square.

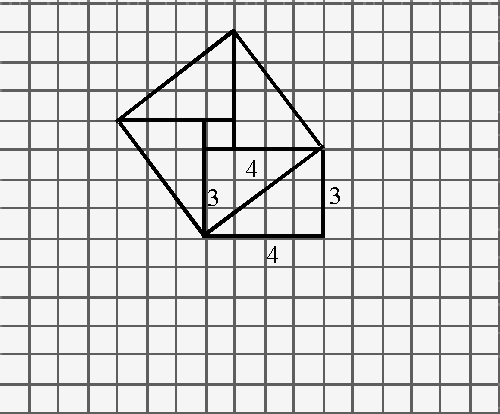
Figure 4

Stage 3: Draw squares on each of the other sides of the fifth triangle and find their area.

The area of the square on the side of the triangle with length 3 is 3 x 3 = 9

The area of the square on the side of the triangle with length 4 is 4 x 4 = 16

The area of the rectangle is 4 x 3 = 12

The area of a triangle is 12 ¸ 2 = 6

The area of four triangles is 4 x 6 = 24

The area of the middle square is 1

The area of the square on the hypotenuse of the triangle is 24 + 1 = 25

ie. 25 units of the Sum-copy squares.

Figure 5

Stage 4: Notice the connection which appears between the areas of the squares:

the areas of the two smaller squares total to give the area of the single larger square.

Short² + Short² = Long²

Area 9 + Area 16 = Area 25

The area of the square on the hypotenuse of a right-angled triangle

is equal to

the sum of the areas of the squares on the other two sides of the triangle.

This connection is known as Pythagoras Theorem

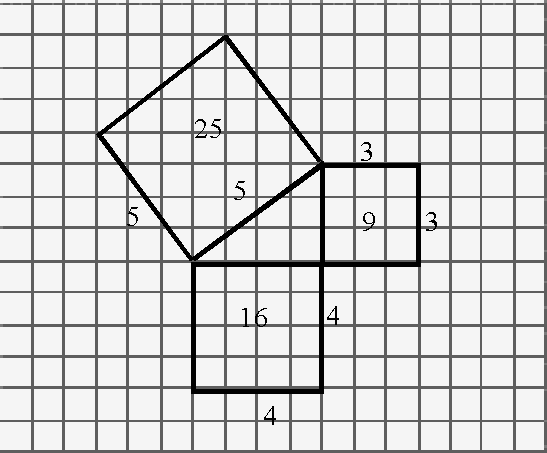
Figure 6

Development 1: The exact length of the side of the large square can now be found without using a ruler if we wish.

The side length must be a number which divides the same number of times as itself into 25:

ie. the answer is the square root of 25 which is 5

We can write √25 = 5 is the length of the hypotenuse of the triangle.

Development 2:

This method may be used with any two lengths of sides of a right-angled triangle.

Notice that in cases where two sides of the same length are used there is no ‘middle square’.

Home

Page by N.Hallinan ©2006